CS224d笔记5——递归神经网络（Recusive Neural Network, RNN）

这部分介绍递归神经网络（RNN），递归神经网络通过在一个结构上递归地应用同一组参数来预测任意输入的结构，或者通过遍历输入的拓扑结构产生一个标量输出来创建网络。上篇文章介绍的循环神经网络可以看成时间上的递归，可以看成是结构递归的一种简化版递归神经网络。

RNN适用于有嵌套层次和内在递归结构的任务。目前RNN在NLP领域的应用主要有句法分析和句子表示。假设一个句子的含义是由句子中词的含义和词的组合方式决定的，word2vec已经一定程度上说明可以用向量来表示词的含义，词的组合规则从句法的角度来看可以理解成句法树，我们可以通过遍历句法树来构建RNN（递归的时候使用同一组参数）来生成句子的表示。这样生成句子、短语的表示考虑了词的顺序、词的组合和词的含义。其实我们可以利用RNN来同时学习句子的句法结构和句子的向量表示。

RNN用于结构预测的时候需要用到一个max-margin目标函数，暂时没有看懂这个目标函数。所以本文仅介绍在有一个句法树的前提下来生成句子表示的过程，同时结合一个简单的情感分析任务来解释RNN的前向传播和反向传播过程。

单层RNN建模情感分析

现在用一个简单的RNN来建模情感分析任务，学习句子的表示。假设我们现在已经有了句子的句子分析树和词表示，如下图所示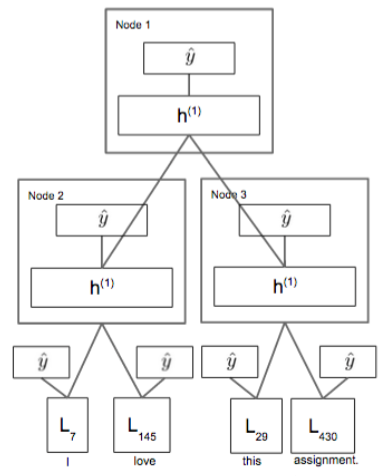： LSTM RNN 假设词表示的维度$L_i\in \mathbb{R}^d$，为了得到Node3节点的表示，我们将这个节点的两个孩子节点的表示$L_{29}$和$L_{430}$拼接起来，输入一个只有一个隐藏层的神经网络，得到Node3节点的表示：

$$h^{(1)}=\tanh(W^{(1)} \begin{bmatrix} L_{29}\\ L_{430} \end{bmatrix} + b^{(1)}) $$

其中$W^{(1)}\in \mathbb{R}^{d\times 2d}$，$b^{(1)}\in \mathbb{R}^d$，$h^{(1)}\in \mathbb{R}^d$。可以把$h^{(1)}$看作是the assignment的表示，RNN的优势在于不需要直接学习Bigram的表示，通过现有的词表示和词组合方式就可以推导出短语的表示。得到$h^{(1)}$之后可以接一个softmax 进行分类，以情感分类的例子为例，可以分5类：Really Negative, Negative, Neutral, Positive, Really Positive。

同样的方式可以得到I love的短语表示。接着根据I love和the assignment的短语表示就可以得到整个句子的短语表示，计算方式如下：

$$h^{(1)}=\tanh(W^{(1)} \begin{bmatrix} h_{left}^{(1)}\\ h_{right}^{(1)} \end{bmatrix} + b^{(1)}) $$

$$\hat{y}=\text{softmax}(Uh^{(1)}+b^{(s)}) $$

$h_{left}^{(1)}$是左孩子的输出向量，$h_{left}^{(1)}$是右孩子的输出向量（这两个向量都可能是词向量）。最后经过一个softmax得到整个句子的分类，在情感分类任务中 $U\in \mathbb{R}^{5\times d}$，$b^{(s)}\in\mathbb{R}^5$。

前向传播过程实际上就是用一个深度优先遍历就可以完成，步骤如下：

得到左孩子的表示
得到右孩子的表示
得到根节点的表示

后向传播

需要注意的是在RNN中我们在每个节点用的参数都是一样的，求导的时候和普通神经网络的区别在于我们只需要把每个节点的参数的梯度累加起来就可以了。

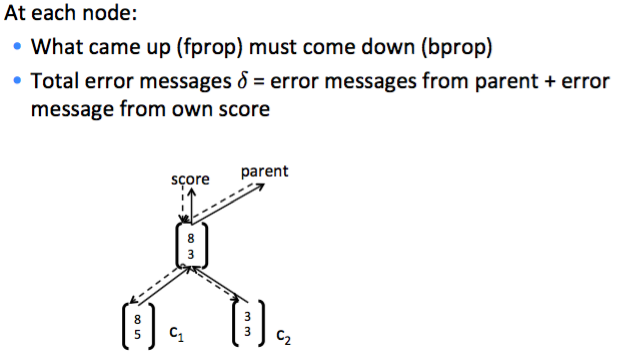
此外还有两点需要注意，一是父节点的输入时由两个子节点的输出拼接而成的，当父节点的误差往子节点传播的时候需要切成两份： LSTM RNN 二是每个节点的$h^{(1)}$处的误差来源有两个部分，一个是softmax传回来的，一个是父节点传回来的：

整个后向传播过程也是一个深度优先遍历，步骤如下：

计算根节点的误差
计算左孩子的误差
计算右孩子的误差

下面以上节提到的情感分析的例子来描述一下整个后向传播过程。前文可知，RNN中每个节点都进行了一次softmax分类，每个节点输出的情感分类的损失可以用交叉熵度量：

$$\text{CE}(y,\hat{y})=-\sum_i y_i\log(\hat{y}_i)$$

根据上文的句法结构，RNN在后向传播的时候，先计算Node1的误差，然后Node2，最后 Node3，得到$W^{(1)}$、$b^{(1)}$、$U$、$b^{(s)}$和$L$的更新公式。

对于内部节点Node1~3无法直接和词表中的向量$L$交互，所以Node1~3只需要对 $W^{(1)}$、$b^{(1)}$、$U$、$b^{(s)}$求误差。$\delta_{above}$是父节点传给当前的误差， $\delta_{below}$是当前节点传递给子节点的误差，拆成两个部分分别传递给左右孩子。 RNN后向传播

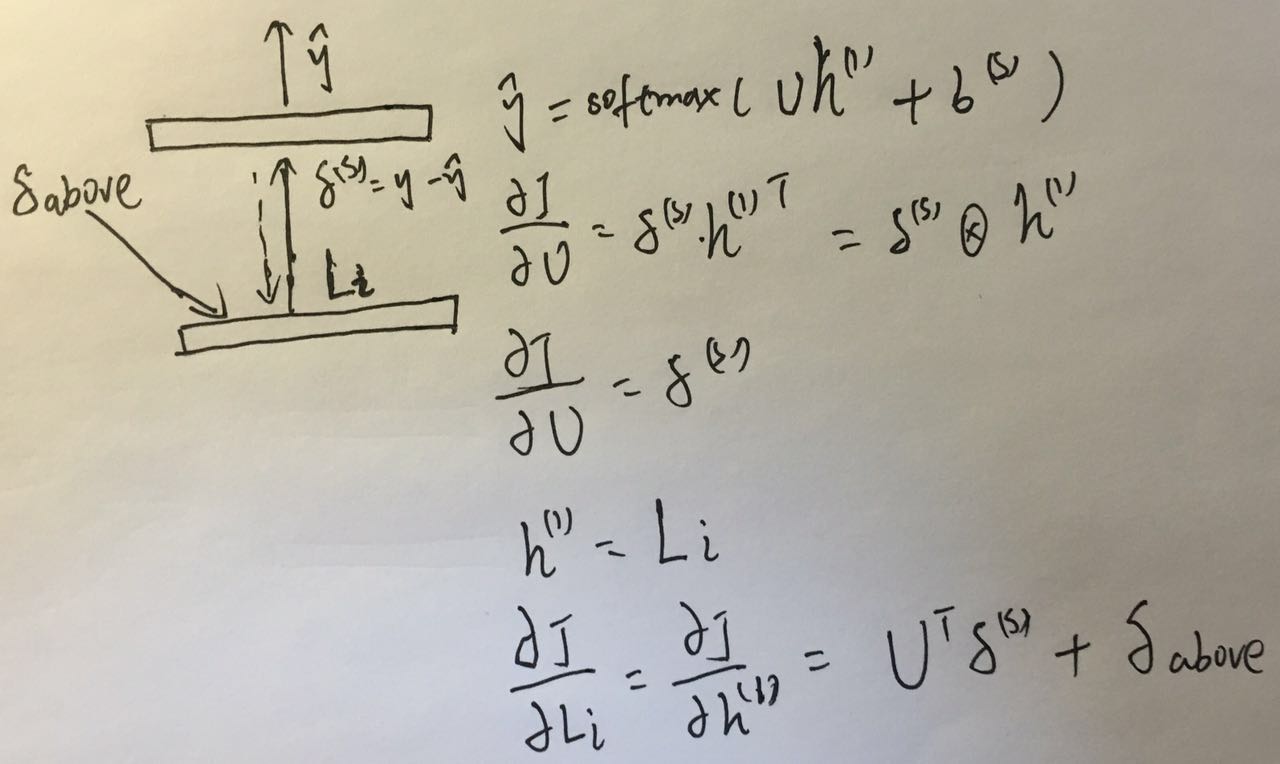
对于叶子节点求误差就比较简单，只需要对$U$、$b^{(s)}$和叶子节点对应的词$L_i$求误差就行。 RNN叶子后向传播

最后要做的就是把各个节点中求得的各个参数的误差累加起来，得到所有参数的梯度，进行参数更新。

RNN改进

上面描述的RNN有一个很严重的问题是，在每个节点计算$h^{(1)}$的时候都使用相同的$W^{(1)}$ 把两个孩子的表示拼接起来，很明显的是我们在拼接冠词和名词的时候用的$W$应该和拼接名词和动词用的$W$应该不一样。

Syntactically Untied SU-RNN

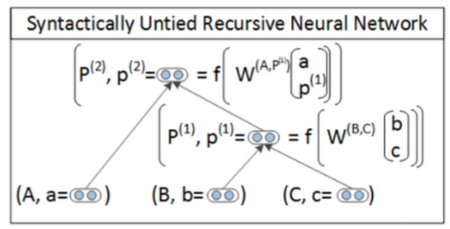
SU-RNN的主要思想是用PCFG先给句法树种的每个节点和词打上标签。然后DT-NP拼接的时候用一种$W$，VP-NP拼接的时候用另一个$W$，这样可以提高模型的描述能力。 SU-RNN

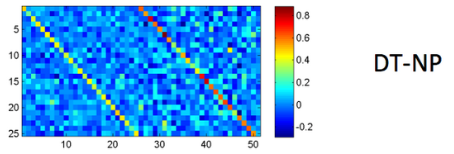
这个模型在训练的时候要把$W\in \mathbb{R}^{2d}$初始化成单位矩阵，相当于初始的时候两个子节点的向量拼接就是把两个向量对应维度相加。最后通过模型能够学习出来两种类型的子节点拼接哪个更重要一点，例如DT-NP拼接（The cat或者A man）的时候NP会更重要一点，下图是一个真实学习到的矩阵： SU-RNN

SU-RNN比之前的同一个$W$的模型有了一定的改进，但是还解决不了修饰词的问题，例如very 这个词会本身就会使得另一个词的词意变强，通过SU-RNN的这种线性插值的方法无法让某个向量去放大另一个向量。界面介绍两个可以描述这类问题的模型MV-RNN和RNTN。

MV-RNN’s (Matrix-Vector Recursive Neural Networks)

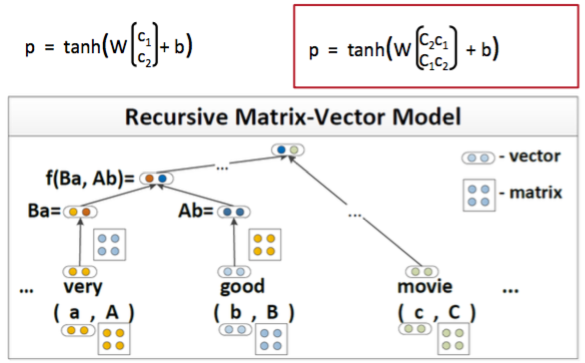
MV-RNN中每个词不仅有一个词向量，还有一个矩阵，例如下图中的词very有一个向量a 还有一个矩阵A。当very和good组合的时候首先需要把当前词的向量和另一个词的矩阵相乘，例如very的向量a需要和good的矩阵B相乘，然后再通过普通RNN的计算公式得到新节点的隐藏层表示。very这个词的矩阵可以初始化成单位矩阵乘上某个正数，这样和对方的向量相乘的时候就可以放大对方的向量。

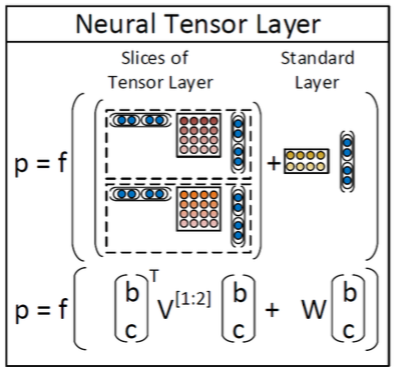
MV-RNN

RNTNs (Recursive Neural Tensor Network)

RNTN首先对左右孩子的$h^(1)$进行拼接得到$x\in\mathbb{R}^{2d}$，在普通的RNN中也这么做但是普通的RNN直接把$x$进行线性变化之后就经过非线性神经单元，而在RNTN中首先对$x$进行一次二次变换，然后加上线性变换，最后通过非线性单元：

$$h^{(1)}=\tanh(x^TVx + W^{(1)}x)$$

其中$V\in\mathbb{R}^{2d\times 2d\times d}$是一个三阶的张量（Tensor）。 $x^TVx$的计算方式是把张量的每一个分片（张量的一个分片维度是$\mathbb{R}^{2d\times 2d}$） $V[i],i\in[1,2,\ldots,d]$对$x$计算$x^TV[i]x$，最后输出一个$\mathbb{R}^{d}$的向量。然后加上一个$W^{(1)}x$，然后通过一个非线性变换。通过二次变换实际上两个向量之间进行了乘法类型的交互，而且不需要像MV-RNN一样对每个词保持一个矩阵，参数空间小了很多。