CS224d笔记1——word2vec — Life in a Nutshell

假期学习了斯坦福的CS224d课程，该课程的主要内容是神经网络在自然语言处理领域的应用。这里记录相关的学习笔记，大概分成以下几个部分：word2vec，窗口分类，神经网络，循环神经网络，递归神经网络，卷积神经网络。

为什么需要深度学习

传统的机器学习方法都是认为的设计特征或者表示，深度学习的目的是希望能够通过神经网络让机器自动学习到有效的特征表示，这里所说的深度学习更偏向于关注各种类型的神经网络。探索机器学习的原因主要有以下几方面：

人工设计的特征常常定义过多，不完整并且需要花费大量的时间去设计和验证
自动学习的特征容易自适应，并且可以很快的学习
深度学习提供了一个弹性的，通用的学习框架用来表征自然的，视觉的和语言的信息。
深度学习可以用来学习非监督的（来自于生文本）和有监督的（带有特别标记的文本，例如正向和负向标记）
在2006年深度学习技术开始在一些任务中表现出众，为什么现在才热起来？
- 深度学习技术受益于越来越多的数据
- 更快的机器与更多核CPU/GPU对深度学习的普及起了很大的促进作用
- 新的模型，算法和idea层出不穷
通过深度学习技术提升效果首先发生在语音识别和机器视觉领域，然后开始过渡到NLP领域

深度学习在所有的NLP层次（音素、形态学、句法、语义）都得到了应用，在所有的NLP层次的表示都涉及到向量（Vectors），下面主要讲如何用向量来表示词。

词向量

在传统意义上会使用WordNet来表示词的含义，通过WordNet可以查询词之间的上下位关系、一个词的同义词、度量词之间的相似度等。但是WordNet是由人工维护，存在一些问题：

语义词典资源很棒但是可能在一些细微之处有缺失，例如这些同义词准确吗：adept, expert, good, practiced, proficient,skillful?
新词缺失（无法及时更新）
人为构建，具有一定的主观性
需要耗费大量的人力来构建
很难用来计算词与词的相似度

One-hot向量

首先我们把词表中的词从0到$|V|-1$进行编号，ont-hot向量把每个词表示成一个$|V|$维（词表大小为$|V|$）的向量，该向量只有特定词的编号对应的位置为1，其他位置全部为0 。这种方法把每个词表示成独立的个体，无法通过one-hot向量直接到词之间的关系。解决方法是通过一个词的上下文来表示一个词。

基于SVD分解的方法

这种方法的基本思想是通过大量的数据统计到词的累计共现矩阵$X$，然后对$X$进行奇异值分解得到$USV^T$，$U$的每一行对应一个词的向量表示，SVD更多信息参考这里。共现矩阵一般分为词-文档共现矩阵和词-词共现矩阵。

词-文档共现矩阵

这种共现矩阵的思想认为相关的词会出现在同一个文档中。假设词表大小为$|V|$，文档数量为$|M|$，那么词-文档共现矩阵规模为$|V|\times|M|$，矩阵元素$X_{ij}$表示词i在文档j中的出现次数，只要对所有文档循环一次就可以统计得到该矩阵

词-词共现矩阵

词-词共现矩阵的思想是词i的窗口内出现了j，那么认为i和j的共现次数加一，$X_{ij}$表示两个词的共现次数，$X$是一个$|V|\times|V|$的方阵。窗口一般是对称的，长度一般为 5-10。下面举一个简单的例子，例子中窗口大小为1，语料如下：

I enjoy flying.
I like NLP.
I like deep learning.

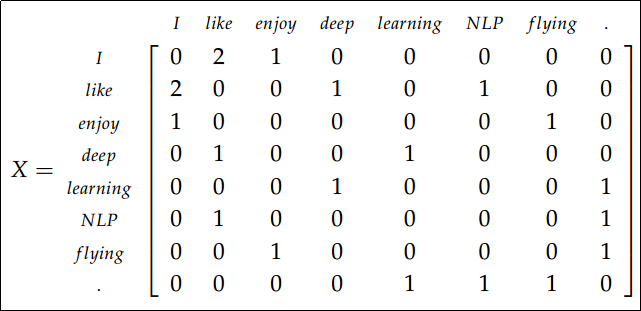
得到共现矩阵如下：词-词共现矩阵

对该矩阵进行SVD分解： svd

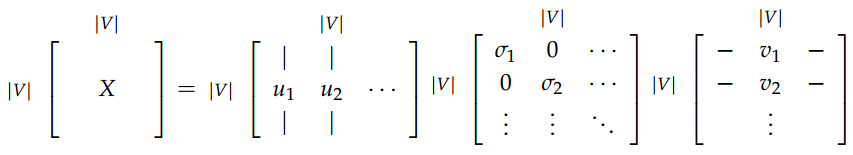
之后区$U$的前$k$列作为所有单词的$k$维向量表示。

这种基于共现矩阵进行SVD分解的方法存在问题：

矩阵的维度经常发生变化（新词和新文档的加入）
矩阵非常稀疏
矩阵过大
SVD分解的计算复杂度大，对于$n\times m$的矩阵进行分解的复杂度为$O(mn^2)$
需要对$X$矩阵进行一些修正来修复词频分布不均匀问题

对$X$矩阵的一些修正：

功能词(the, he, has)过于频繁，对语法有很大影响，解决办法是降低使用或完全忽略功能词
采用带权重的窗口，距离当前词距离越近共现权重越大
用皮尔逊相关系数代替计数，并置负数为0

Word2vec

Word2vec的基本思想与共现计数不同，word2vec主要分为两种，采用当前词来预测窗口中的其他词（skip-gram），另一种是用窗口中的词来预测当前词（cbow）。

CBOW

CBOW（Continuous Bag of Words）的基本思想是用窗口中的词的向量求平均之后来预测中心词。训练语料是上下文和对应的中心词的对，上下文窗口内的每个词都用一个one-hot向量 $x^(i)$表示，中心词用one-hot向量$y^(i)$表示，CBOW中预测的中心词只有一个所以直接把输出向量表示成$y$。

随机初始化两个矩阵（一般用正态分布进行初始化）$W^{(1)}\in \mathbb{R}^{n\times |V|}$和 $W^{(2)}\in \mathbb{R}^{|V|\times n}$分别用来存储输入向量和输出向量，最后训练完每个词有两个向量，一个是当作输入时的向量，一个是当作输出时的向量。$n$为词向量的维度；$W^{(1)}$ 的第$i$列表示词$w^(i)$当作输入时的向量表示，记作$u^{(i)}$；$W^{(2)}$的第$j$行表示词$w^(j)$当作输出时的向量表示，记作$v^{(j)}$。利用上下文预测中心词的步骤如下：

把大小为$C$的上下文用one-hot向量表示 $(x^{(i-C)},\ldots,x^{(i-1)},x^{(i+1)},\ldots,x^{(i+C)})$
把$W^{(1)}$分别和$2C$个one-hot向量相乘，得到上下文的输入向量，例如 $x^{(i-C)}$作为输入时的向量为$u^{(i-C)}=W^{(1)}x^{(i-C)}$
将上下文中的向量进行平均$h=\frac{u^{(i-C)}+u^{(i-C+1)}+\ldots +u^{(i+C)}}{2C}$
生成得分向量$z=W^{(2)}h$
利用softmax函数将得分转换成概率$\hat{y}=\text{softmax}(z)$
我们的目标是希望预测的概率$\hat{y}$和真实的中心词one-hot向量$y$一致

我们希望模型输出的概率分布和真实分布的尽量相似，可以利用信息论中的交叉熵来衡量两个概率分布的距离，离散情况下两个概率分布的交叉熵$H(\hat{y},y)$如下：

$$H(y,\hat{y})=-\sum_{j=1}^{|V|}y_j\log(\hat{y}_j)$$

考虑CBOW中的情况，此时$y$是一个one-hot向量，假设$y$的第$i$维为1，那么交叉熵可以简化成：

$$H(y,\hat{y})=-y_i\log(\hat{y}_i)=-\log(\hat{y}_i)$$

可以看出交叉熵的最小值为0，优化目标就是最小化交叉熵：

\begin{align*} \min J&=-\log P(w^{(i)}|w^{(i-C)},\ldots,w^{(i-1)},w^{(i+1)},\ldots,w^{(i+C)})\\ &=-\log P(v^{(i)}|h)\\ &=-\log \frac{\exp{(v^{(i)}\cdot h)}}{\sum_{j=1}^{|V|}\exp(v^{(j)}\cdot h)}\\ &=-v^{(i)}\cdot h + \log{\sum_{j=1}^{|V|}\exp(v^{(j)}\cdot h)} \end{align*}

由上描述可知整个模型的未知参数就是$W^{(1)}$和$W^{(2)}$，即对于每个输出向量$v^{(j)}$和上下文中的输入向量$(u^{(i-C)},\ldots,u^{(i-1)},u^{(i+1)},\ldots,u^{(i+C)})$求导。

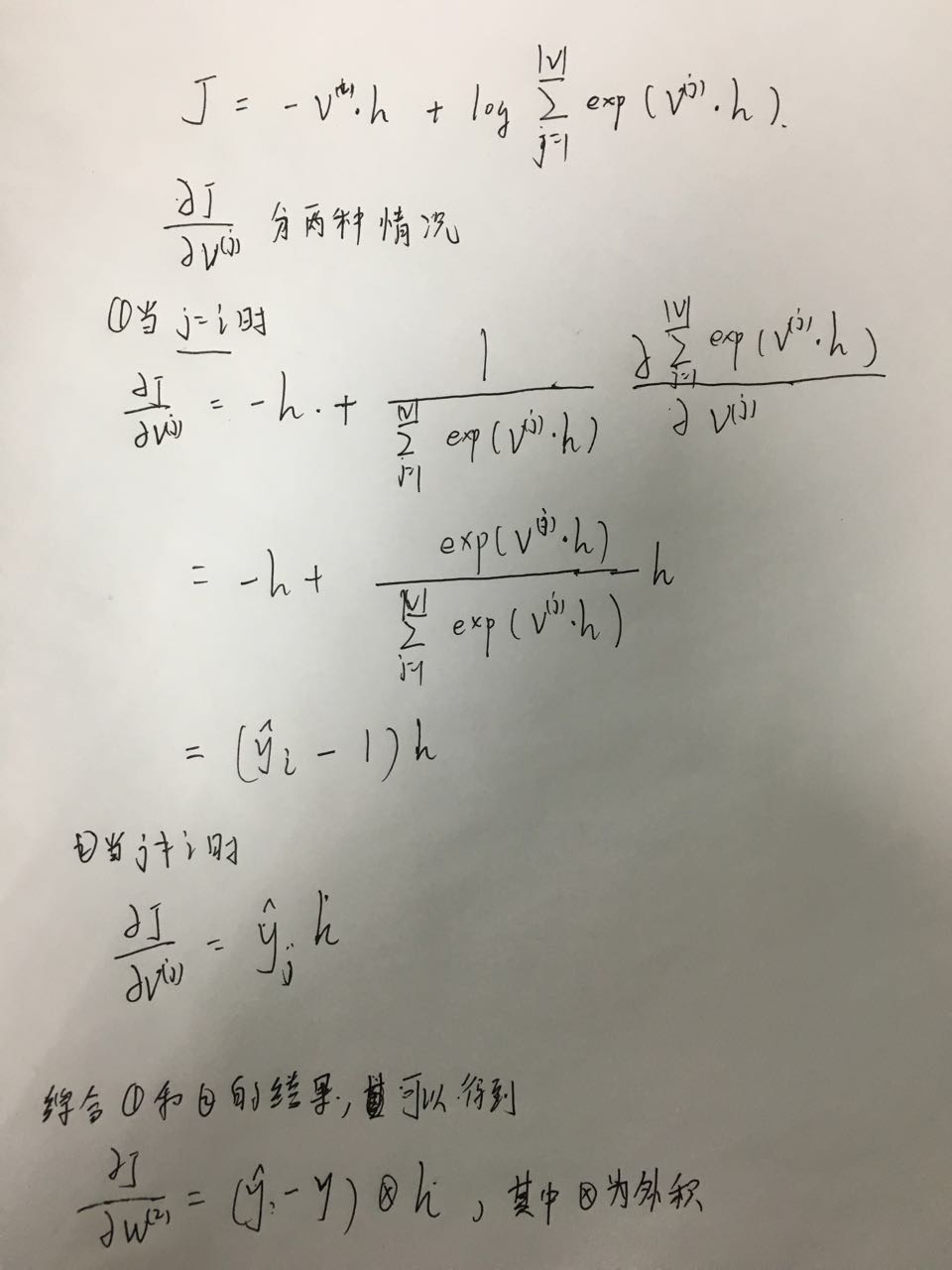
首先是$\frac{\partial J}{\partial v^{(j)}}$ J对输出向量求导

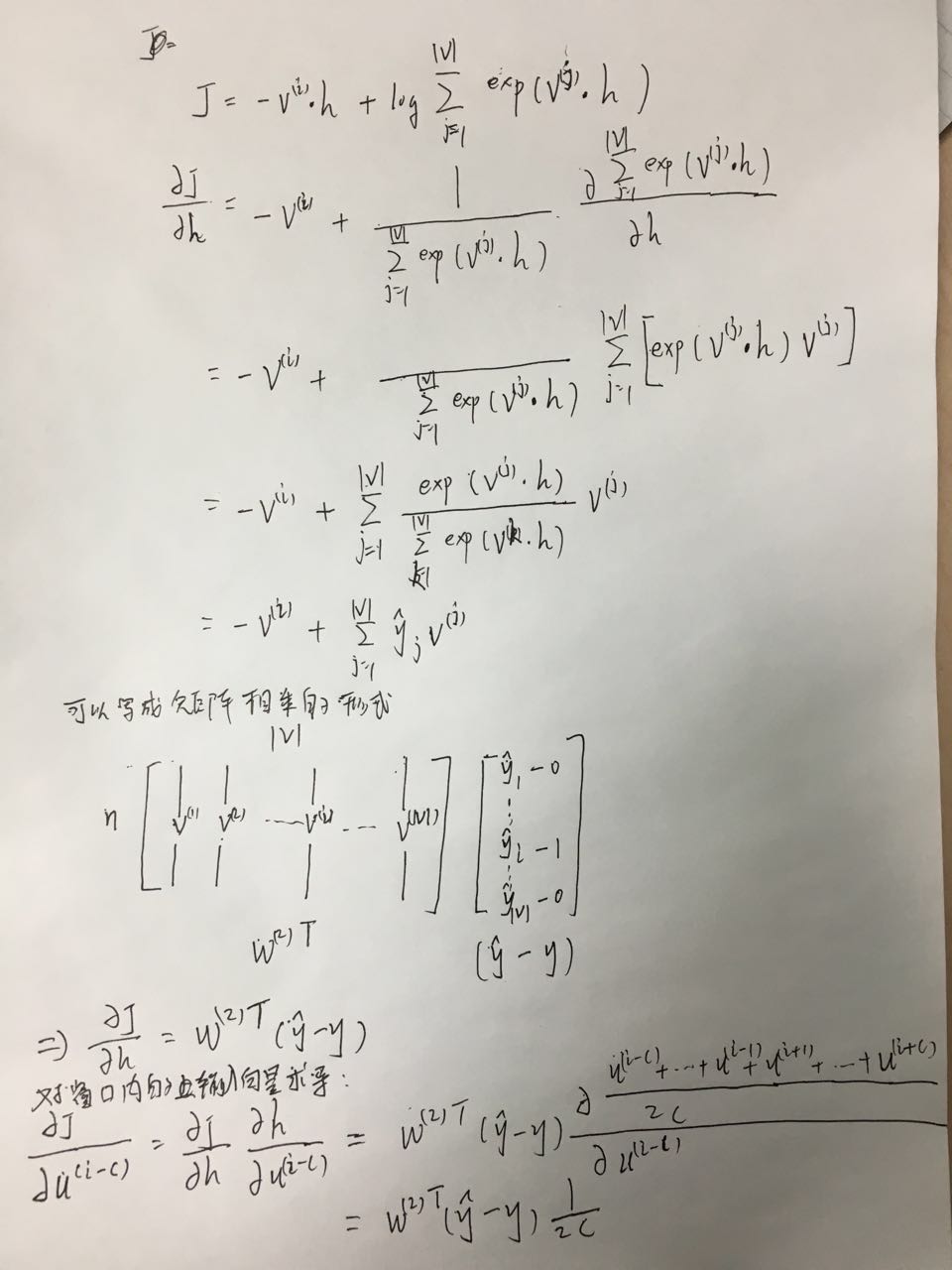
然后对窗口内的其中一个输入向量求导$\frac{\partial J}{\partial u^{(i-C)}}$，其他输入向量求导方法与之相同，最后结果相等 J对输出向量求导

Skip-Gram

Skip-Gram的基本思想用当前词预测窗口长度为$C$内的其他词，此时模型的输入是中心词one-hot 向量$x$，窗口内的词one-hot向量为$(y^{(i-C)},\ldots,y^{(i-1)},y^{(i+1)},\ldots,y^{(i+C)})$。利用中心词预测周边词的过程如下：

输入one-hot向量为$x$
$x$的输入向量表示为$u^{(i)}=W^{(1)}x$
只有一个输入所以不需要像CBOW一样对向量进行平均，$h=u^{(i)}$
生成得分向量$z=W^{(2)}h$
利用softmax函数将得分转换成概率$\hat{y}=\text{softmax}(z)$
我们的目标是希望预测的概率$\hat{y}$和真实的概率$(y^{(i-C)},\ldots,y^{(i-1)},y^{(i+1)},\ldots,y^{(i+C)})$一致

这里把$P(w^{(i-C)},\ldots,w^{(i-1)},w^{(i+1)},\ldots,w^{(i+C)}|w^{(i)})$整体看成一个分布，然后用朴素贝叶斯假设来简化这个条件概率的求解，即：

\begin{align*} \min J&=-\log P(w^{(i-C)},\ldots,w^{(i-1)},w^{(i+1)},\ldots,w^{(i+C)}|w^{(i)})\\ &=-\log \Pi_{j=0,j\neq C}^{2C}P(w^{(i-C+j)}|w^{(i)})\\ &=-\log \Pi_{j=0,j\neq C}^{2C}P(v^{(i-C+j)}|u^{(i)})\\ &=-\log \Pi_{j=0,j\neq C}^{2C}\frac{\exp{(v^{(i-C+j)}\cdot h)}}{\sum_{k=1}^{|V|}\exp(v^{(k)}\cdot h)}\\ &=-\sum_{j=0,j\neq C}^{2C}v^{(i-C+j)}\cdot h + 2C\log{\sum_{k=1}^{|V|}\exp(v^{(k)}\cdot h)}\\ \end{align*}

对于这个损失函数我们可以先不考虑对窗口内的所有词求和，假设我们现在只针对窗口内的特定词$w^{(j)}$进行预测，此时

$$J=-v^{(j)}\cdot h + \log{\sum_{k=1}^{|V|}\exp(v^{(k)}\cdot h)}$$

该损失函数对于每个输出向量的导数的求解结果与CBOW类似，损失函数对于输入向量的求导结果也和CBOW类似。唯一的区别在于skip-gram的输入向量只有一个，所以$J$对于$u^{(i)}$的导数直接为${W^{(2)}}^T(\hat{y}-y)$不需要除以$2C$。

负采样

上述的CBOW和Skip-Gram模型都存在一个问题，就是损失函数都有一个求和是$|V|$规模的，这个计算非常耗时，英文的词汇表规模大概是1300万。负采样是基于Skip-Gram模型，但是和优化目标和Skip-Gram不同。给定一对词$(w,c)$，其中$w$是中心词， $c$代表$w$的上下文窗口内出现的另一个词，用$P(D=1|w,c)$表示$(w,c)$确实出现在语料中的概率，相应的$P(D=0|w,c)$表示$(w,c)$ 没有出现在语料中的概率。用sigmoid函数（下文用$\sigma$表示sigmoid函数）来表示$P(D=1|w,c)$这个概率，这里用 $v_c$表示输出向量，$u_w$表示输入向量。

$$P(D=1|w,c,\theta)=\frac{1}{1+\exp(-v_c^Tu_w)}$$

我们期望优化的目标是希望真实存在语料中$(w,c)$对$P(D=1|w,c)$最大化，同时不存在语料中的$(w,c)$对$P(D=0|w,c)$概率最大化，公式中的$\theta$包括了上面提到的两个矩阵$W^{(1)}$和$W^{(2)}$，我们希望$\theta$满足下列公式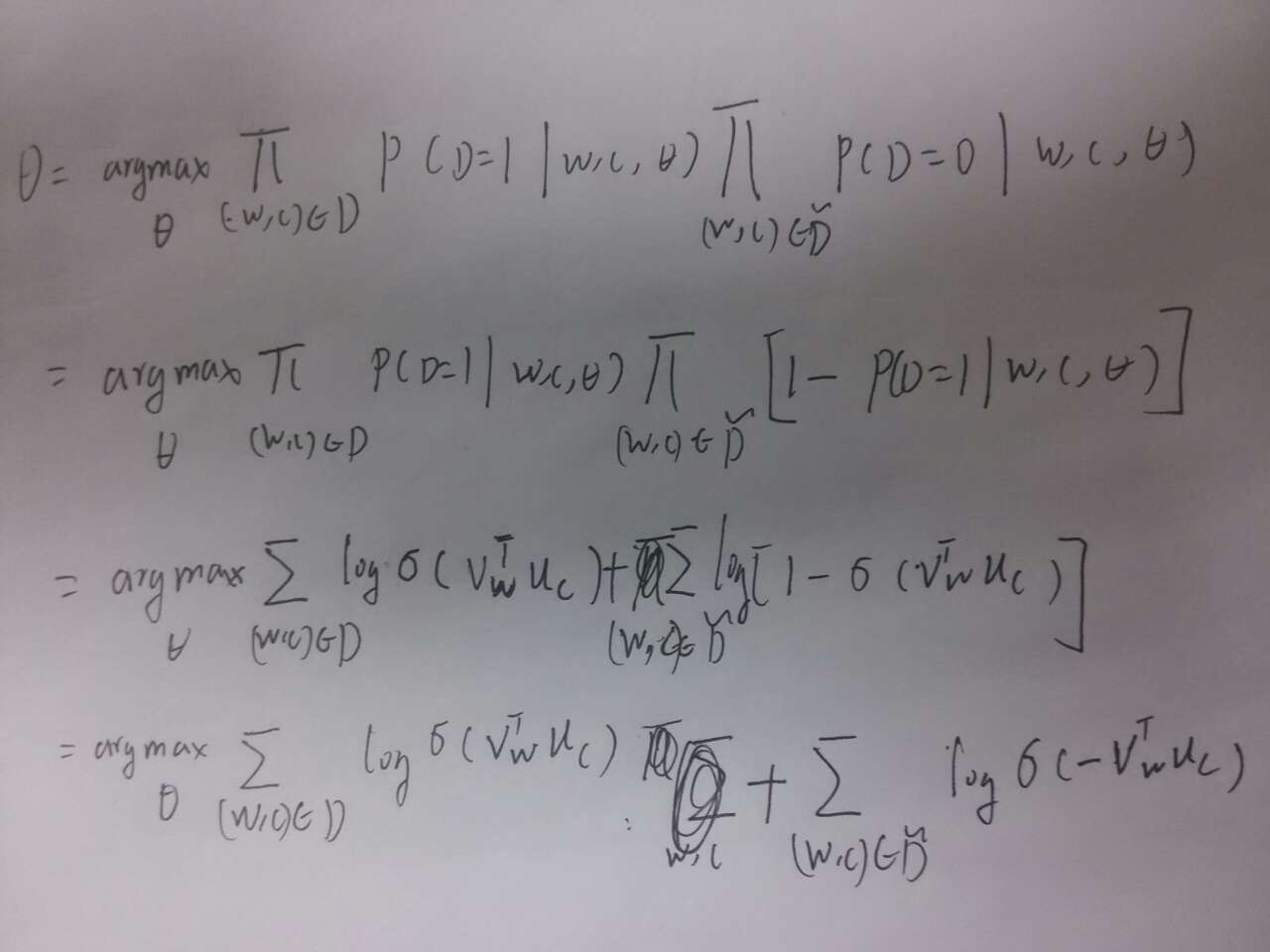：负采样优化目标上述推导中用到需要用到了一个等式$1-\sigma(x)=\sigma(-x)$，这个等式比较好验证，其中$\tilde{D}$为负样本。由此可得新的目标函数

$$\min J=-\log\sigma(v_c^Tu_w)-\sum_{k=1}^{K}\log\sigma(-v_k^Tu_w)$$

在这个目标函数中$v_k$是从$P_n(w)$从采样出来的，这个$P_n(w)$是unigram概率$U(w)$的$3/4$次方，这样可以增大一些概率很小的词被采样出来的概率。

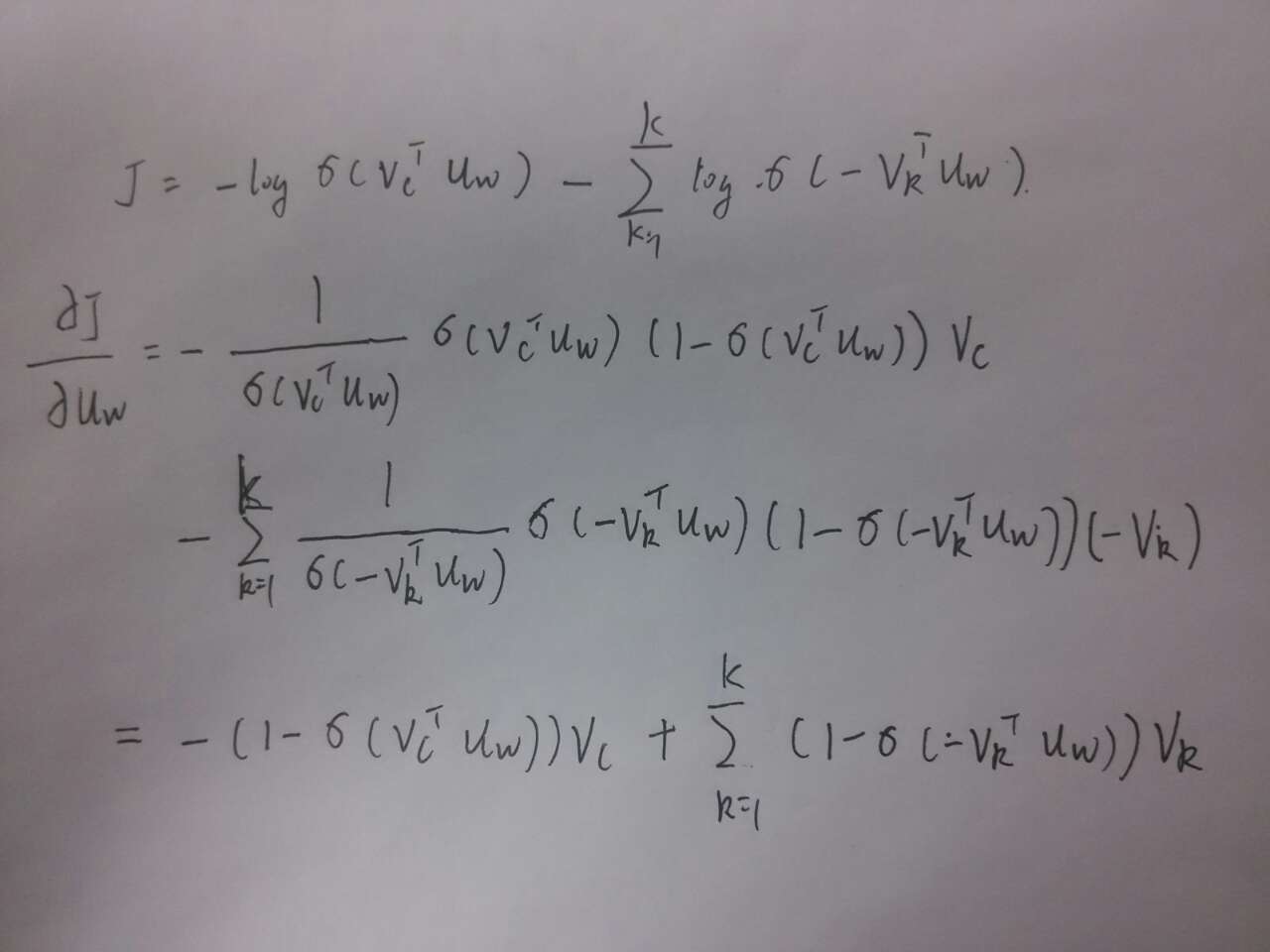
可以求得$\frac{\partial J}{\partial u_w}$ 负采样输入向量梯度

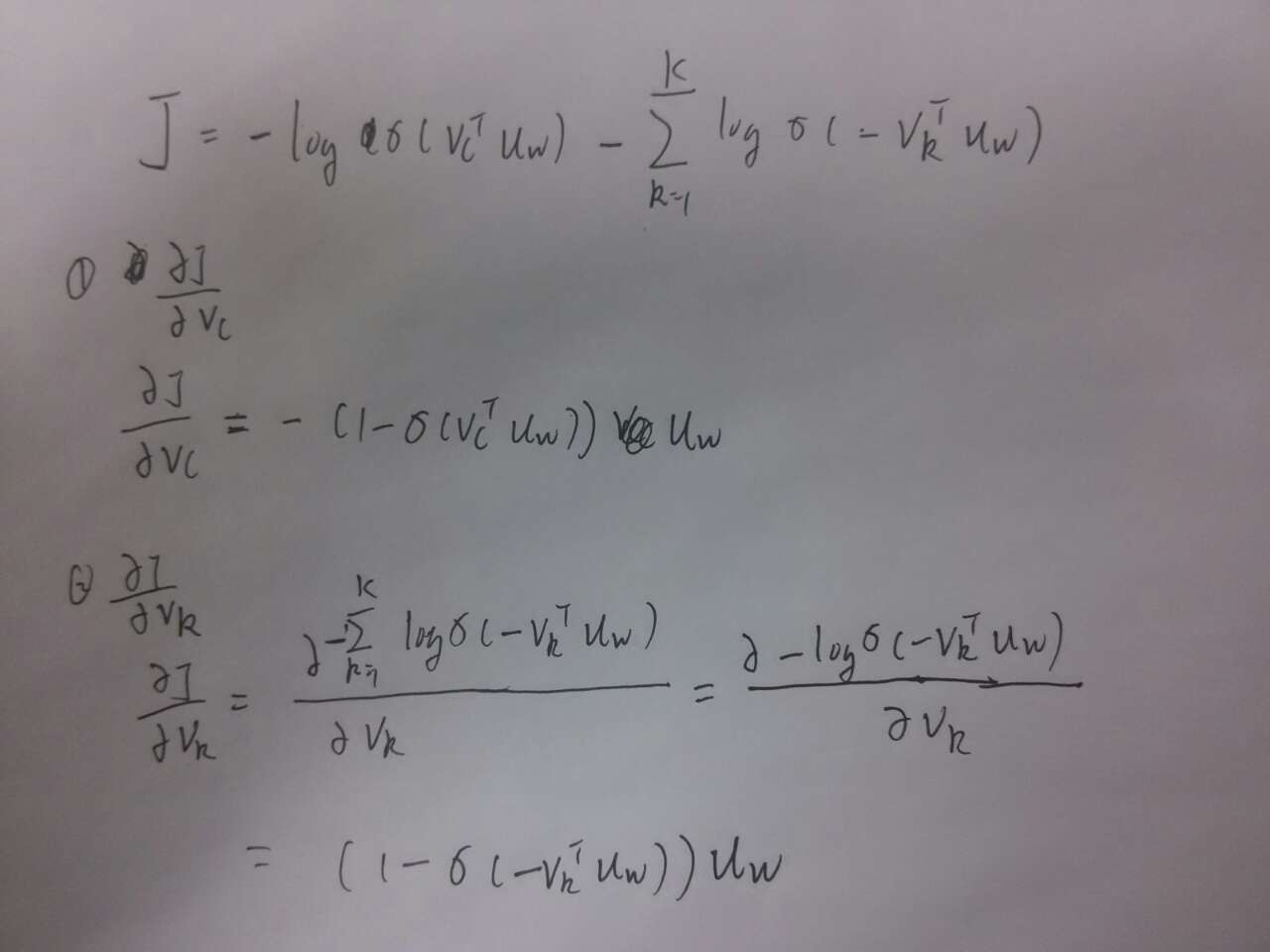
然后是$J$对相关的输出向量求导负采样输出向量梯度

求得梯度之后可以采用随机梯度下降优化目标函数，得到向量表示。上述三种方法训练完成之后对于每个词都会得到两个向量，一个是作为模型输入时的向量，一个是作为模型输出时的向量，最后的向量表示是把这两种向量相加使用，即对于词$w^{(i)}$ 的向量为$v^{(i)}+u^{(i)}$。

词向量评测

词向量的评测方法可以分为内部（intrinsic）评测和外部（extrinsic）评测，两种评测的对比如下：

内部评测：
- 在一个特定的子任务中进行评测
- 计算迅速
- 有助于理解相关的系统
- 不太清楚是否有助于真实任务除非和实际的NLP任务的相关性已经建立起来
外部评测：
- 在一个真实任务中进行评测
- 需要花很长的实际来计算精度
- 不太清楚是否是这个子系统或者其他子系统引起的问题
- 如果用这个子系统替换原有的系统后获得精度提升–>有效(Winning!)

词向量内部评测方法

词向量内部评测方法主要有词向量类比、词向量相关度，这两种方法有相应的数据集。

词向量类比的基本思想如下

目前评测的数据集主要是word2vec项目提供的数据集包含了语义类比和语法类比两种。语义类比的数据有州名包含城市名、首都和国家，语法类比的数据是比较级类比和时态类比。

词向量相关度的数据集例如WordSim353，该数据集是人为地给两个词的相关度打分（从0-10），然后通过计算词向量的Cosine相似度与这个相关度进行对比。

词向量外部评测方法

简单来说就是把词向量应用于具体的任务中来评测不同的词向量对于任务整体性能的影响。这里需要注意的问题是，应用于具体任务的时候是否还需要调整词向量，一般来说调整词向量会降低向量的范化能力。所以一般具体任务的训练集足够大时才考虑调整词向量。