最大熵 — Life in a Nutshell

最大熵原理

最大熵原理指的是当我们在估计概率分布的时候，这个概率分布符合已知信息的约束并且该分布是最均匀的。从熵的角度考虑就是要让这个分布符合约束并且熵最大。

The principle of maximum entropy states that, subject to precisely stated prior data (such as a proposition that expresses testable information), the probability distribution which best represents the current state of knowledge is the one with largest entropy.

现在考虑一个文本分类的例子，假设我们有4个类别的文本分别是：economics、 sports、politics和art。因为文本只能被分成4个类别，假设现在没有额外的信息，那么约束只有以下的1个

$$p(economics)+p(sports)+p(politics)+p(art)=1$$

那么我们希望得到得概率分布尽量均匀，就会得到下面结果

$$p(economics)=p(sports)=p(politics)=p(art)=0.25$$

现在假设我们有一个先验信息是60%的文档是economics或者sports类别的，那么我们的概率分布就会有以下两个约束

$$p(economics)+p(sports)=0.6$$

$$p(economics)+p(sports)+p(politics)+p(art)=1$$

考虑以上两个约束又希望使得我们的分布均匀，将会得到下面的结果

$$ \begin{align} \notag p(economics)&=0.30\cr \notag p(sports)&=0.30\cr \notag p(politics)&=0.20\cr \notag p(art)&=0.20 \end{align} $$

但是随着对数据的观察，可能又会对引入其他约束。这时候需要解决两个问题，首先是如何来定量描述分布的均匀；其次是如何在考虑约束的条件下使得分布均匀。最大熵的基本思路就是选择一个与给定事实一致的模型（满足约束），并且要使得模型对未知事实不做假设（使得分布尽量均匀）。

最大熵建模

我们继续考虑上面提到的文本分类的例子，假设用最简单的词袋模型来表示文档，每个文档都可以表示成一个词频向量，例如下面的简单的例子

Doc1: John likes to watch movies. Mary likes movies too.
Doc2: John also likes to watch football games.

得到词表如下:

{
    "John": 1,
    "likes": 2,
    "to": 3,
    "watch": 4,
    "movies": 5,
    "also": 6,
    "football": 7,
    "games": 8,
    "Mary": 9,
    "too": 10
}

所以可以把Doc1和Doc2表示成两个10维的向量，如下:

Doc1: [1, 2, 1, 1, 2, 0, 0, 0, 1, 1]
Doc2: [1, 1, 1, 1, 0, 1, 1, 1, 0, 0]

我们把当个文档用$x$表示，文档类别用$y$表示，根据上面的描述$y$会有4个类别，跟 Logistic Regression类似，我们要建模一个判别模型$p(y|x)$，即给定一个文档$x$，我们的模型可以得出这篇文档属于特定类别$y$的概率。如果用$\mathcal{P}$ 表示所有的条件概率分布，那么$p(y|x)$就是$\mathcal{P}$中的一个元素。

训练数据

我们可以把的$N$个训练数据表示成$\\{(x_1,y_1),\cdots,(x_N,y_N)\\}$，且

$x_i\in X$，其中$X$表示所有的文档类别
$y_i\in Y$，其中$Y$表示训练文档集合，每个文档用词频向量表示

从训练数据样本中我们可以估计出一个经验的联合概率分布

$$\tilde{p}(x,y)=\frac{1}{N}\times \text{the number of times (x,y) appears}$$

特征和约束

最大熵建模的过程中特征函数（简称特征）主要是为了描述训练样本的统计量，例如建模的时候我们可能会考虑当ball这个词出现的时候，文档属于sports的概率是9/10。

为了描述ball出现时文档属于sports类别的事实我们引入特征函数（指示函数或者特征）

$$ f_{ball,sports} (x,y)=\begin{cases} 1 & \text{if y=sports and ball appears in d} \cr 0 & \text{otherwise} \end{cases} $$

考虑经验分布$\tilde{p}(x,y)$下$f$的期望值，这个期望值就是我们关注的统计量（如果对上面那个特征函数按照经验分布求期望，得到的东西就是当ball这个词出现的时候文档属于sports的概率），记为

$$ \begin{equation} \tilde{p}(f)\equiv \sum_{x,y}{\tilde{p}(x,y)f(x,y)} \end{equation} \label{eq:empricalException} $$

其实样本的任何统计量都可以通过特征函数的期望值来表示。

如果我们发现了一些有用的统计量，我们就可以要求我们的模型也要遵循这个信息。我们通过约束模型在特征函数$f$上的期望值来遵循这个统计量，对于模型$p(y|x)$特征函数 $f$的期望值为

$$ \begin{equation} p(f)\equiv \sum_{x,y}{\tilde{p}(x)p(y|x)f(x,y)} \label{eq:modelException} \end{equation} $$

其中$\tilde{p}(x)$是训练样本中$x$的经验分布。我们通过约束模型下特征函数的期望值等于样本中特征函数的期望值，如下所示

$$ \begin{equation} p(f) = \tilde{p}(f) \label{eq:constriant} \end{equation} $$

把前面的$\ref{eq:empricalException}$，$\ref{eq:modelException}$和 $\ref{eq:constriant}$综合起来得意得到下面的约束

$$ \sum_{x,y}{\tilde{p}(x)p(y|x)f(x,y)} = \sum_{x,y}{\tilde{p}(x,y)f(x,y)} $$

这样我们只需要考虑那些满足$\ref{eq:constriant}$的模型$p(y|x)$。总的来说我们用$\tilde{p}(f)$表示样本数据中的统计特征，同时也要求我们的模型要表示出这种特征（$p(f)=\tilde{p}(f)$）。

假设我们现在有$n$个我们认为很重要的特征函数$f_i$，我们希望我们的模型遵循这些特征在训练数据中所表现出的统计信息，那么$p$就应该是$\mathcal{P}$的一个子集 $\mathcal{C}$，定义如下

$$ \begin{equation} \mathcal{C} = \big\{p \in P \text{ | } p(f_i)=\tilde{p}(f_i) \text{ for i } \in \{1,2,\cdots,n\}\big\} \label{eq:distsubset} \end{equation} $$

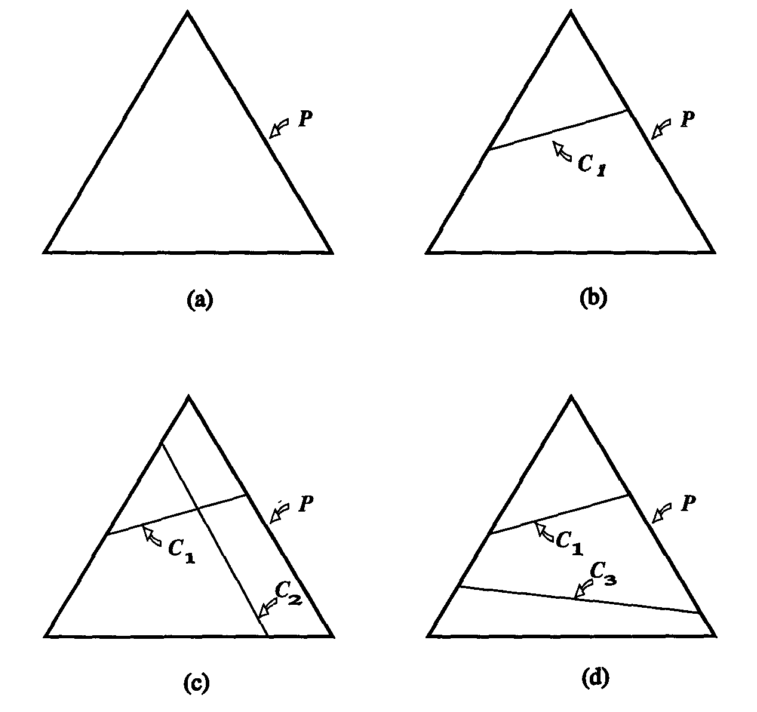
下图解释为概率分布添加约束的过程，图中$\mathcal{P}$表示一个在3个变量上的概率分布，如果我们没有设置任何约束那么所有的概率分布都是可以的如图(a)所示；如果我们添加一个线性约束$\mathcal{C}_1$那么我们的概率分布只能落在图(b)中$mathcal{C}_1$ 这个线上面；此时如果再添加一个约束我们就能确定概率分布$p$，如果第二个线性约束 $\mathcal{C}_2$和$\mathcal{C}_1$不冲突（有交点），那么这个交点就是我们要求的概率分布$p$，如图(c)所示；如果两个约束冲突，例如第一个约束要求第1点的概率是$1/3$ 而第二个约束是要求第3点的概率是$3/4$，那么会得到图(d)的结果。由于我们的约束都是从训练样本中抽取的，所以约束之间不可能冲突，而且我们的约束无法像图(c)一样唯一确定$p$，换句话说$\mathcal{C}=\mathcal{C}_1\cap\mathcal{C}_2\cdots\cap\mathcal{C}_n$ 所确定的模型有无数个。 simplex

在所有的模型$p\in\mathcal{C}$中我们需要根据最大熵原理选择一个最均匀的，我们用条件熵量化度量条件分布$p(y|x)$的均匀程度

$$ \begin{equation} H(p)\equiv -\sum_{x,y}{\tilde{p}(x)p(y|x)\log{p(y|x)}} \label{eq:conditionalentropy} \end{equation} $$

条件熵的取值其下界是0（没有不确定性），上界是$\log{|Y|}$（在所有$y$的取值上均匀分布）。我们的目的就是要从$\mathcal{C}$里面找到一个模型$p^*\in\mathcal{C}$使得$H(p)$最大，即

$$ \begin{equation} p^*= \mathop{\arg\,\max}\limits_{p\in\mathcal{C}}H(p) \end{equation} $$

指数形式

经过上节的分析其实可以知道最大熵模型的目的就是要找到一个模型 $p^*\in\mathcal{C}$使得$H(p)$最大。这其实就是一个有约束条件下的最优化问题，可以用拉格朗日乘数法来解，原始优化问题形式如下：

$$ \begin{align*} & max_p && H(p) \\ & s.t. && p(y|x) \leq 0\text{ for all }x,y.\\ &&& \sum_yp(y|x)=1\text{ for all }x. \\ &&& \sum_{x,y}\tilde{p}(x)p(y|x)f(x,y)=\sum_{x,y}\tilde{p}(x,y)f(x,y)\text{ for } i\in\left\{1,2,...,n\right\}. \end{align*} $$

前两个约束保证模型是一个条件概率分布，第三个约束值得是模型需要满足的统计量。该问题等价于在相同约束下最小化$-H(p)$：

$$\begin{equation}\begin{split} & min_p && -H(p) \\ & s.t. && p(y|x) \leq 0\text{ for all }x,y.\\ &&& \sum_yp(y|x)=1\text{ for all }x.\\ &&& \sum_{x,y}\tilde{p}(x)p(y|x)f(x,y)=\sum_{x,y}\tilde{p}(x,y)f(x,y)\text{ for } i\in\left\{1,2,...,n\right\}. \end{split} \label{eq:primal} \end{equation}$$

用拉格朗日乘数法将有约束问题转换成无约束问题，拉格朗日方程如下：

$$\begin{equation}\begin{split} \mathcal{L}(p,\Lambda,\gamma)=&\sum_{x,y}\tilde{p}(x)p(y|x)\log p(y|x)\\ &+\sum_i^n\lambda_i\left(sum_{x,y}\tilde{p}(x,y)f_i(x,y)-\sum_{x,y}\tilde{p}(x)p(y|x)f_i(x,y)\right)\\ &+\gamma(\sum_yp(y|x) - 1) \end{split} \label{eq:lagrangian} \end{equation}$$

对于$\ref{eq:lagrangian}$这个拉格朗日方程原问题如下：

$$\begin{equation} \min_w\max_{\Lambda,\gamma}\mathcal{L}(p,\Lambda,\gamma) \end{equation}$$

对偶问题为：

$$\begin{equation} \max_{\Lambda,\gamma}\min_w\mathcal{L}(p,\Lambda,\gamma) \label{eq:dual} \end{equation}$$

由于$p$是一个凸函数，并且两个约束都和$p$呈线性关系，所以原始问题的解和对偶问题的解是等价的，下面求如何最大化对偶问题$\ref{eq:dual}。首先固定$Lambda$和 $\gamma$求$\mathcal{L}(p,\Lambda,\gamma)$的最小值，将$\ref{eq:lagrangian}$对 $p$求导，另求导结果等于0，得到：

$$ \frac{\partial \mathcal{L}(p,\Lambda,\gamma)}{\partial p(y|x)}=\tilde{p}(x)\left(1+\log p(y|x)\right)-\sum_i\lambda_i\tilde{p}(x)f_i(x,y) + \gamma=0 $$

可以求得最优的$p(y|x)$具有如下形式：

$$\begin{equation}\begin{split} &\log p^*(y|x)=\sum_i\lambda_if_i(x,y)-\frac{\gamma}{\tilde{p}(x)}-1\\ \Rightarrow&p*(y|x)=\exp\left(\sum_i\lambda_if_i(x,y)\right)\exp\left(-\frac{\gamma)}{\tilde{p}(x)}-1\right) \end{split} \label{eq:optimalp} \end{equation}$$

这样我们就找到了$p^*$的最优化形式，现在的目标就是要去求解$\gamma^*$和 $\Lambda^*$。注意到$\ref{eq:optimalp}$的第二项实际上对应的就是原始束问题 $\ref{eq:primal}$的第二个约束，可以把$\ref{eq:optimalp}$写成如下形式：

$$\begin{equation}\begin{split} p*(y|x)&=\frac{p^*(y|x)}{\sum_yp^*(y|x)}\\ &=\frac{\exp\left(\sum_i\lambda_if_i(x,y)\right)\exp\left(-\frac{\gamma)}{\tilde{p}(x)}-1\right)}{\sum_y{\exp\left(\sum_i\lambda_if_i(x,y)\right)\exp\left(-\frac{\gamma)}{\tilde{p}(x)}-1\right)}}\\ &=\frac{\exp\left(\sum_i\lambda_if_i(x,y)\right)}{Z(x)} \end{split} \label{eq:optimalpnew} \end{equation}$$

其中

$$\begin{equation} Z(x)=\sum_y\exp\left(\sum_i\lambda_if_i(x,y)\right) \end{equation}$$

$\ref{eq:optimalpnew}$就是最终$p^*$的参数形式，并且满足$\ref{eq:primal}$的第二个约束，此时相当于我们已经找到了最优的$p^*$和$\gamma^*$，$p^*$带入拉格朗日方程$\ref{eq:lagrangian}$中，得到对偶函数：

$$ \begin{align} \Psi(\Lambda)&=\mathcal{L}(p^*,\Lambda,\gamma^*)\nonumber\\ &=\sum_{x,y}\tilde{p}(x)p^*(y|x)\log p^*(y|x)+\sum_i^n\lambda_i\left(\sum_{x,y}\tilde{p}(x,y)f_i(x,y)-\sum_{x,y}\tilde{p}(x)p^*(y|x)f_i(x,y)\right)\nonumber\\ &=\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)+\sum_{x,y}\tilde{p}(x)p^*(y|x)\left(\log p^*(y|x)-\sum_i\lambda_i f_i(x,y)\right)\nonumber\\ &=\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x,y}\tilde{p}(x)p^*(y|x)\log Z(x)\nonumber\\ &=\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x}\tilde{p}(x)\log Z(x) \label{eq:optimallambda} \end{align} $$

所以现在的对偶问题$\ref{eq:dual}$相当于是要优化如下目标：

$$ \begin{align} \max_{\Lambda}\Psi(\Lambda)=\max_{\Lambda}\left[\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x}\tilde{p}(x)\log Z(x)\right] \end{align} $$

最优的$\Lambda^*$需要满足：

$$ \begin{align} \DeclareMathOperator*{\argmax}{arg\,max} \Lambda^*=\argmax_{\Lambda}\Psi(\Lambda)=\argmax_{\Lambda}\left[\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x}\tilde{p}(x)\log Z(x)\right] \end{align} $$

最大似然

已知训练数据的经验分布$\tilde{p}(x,y)$，模型$p(y|x)$的对数似然函数表示为：

$$\begin{align} L_{\tilde{p}}(p) &\equiv \log\Pi_{x,y}p(y|x)^{\tilde{p}(x,y)}=\sum_{x,y}\tilde{p}(x,y)\log p(y|x) \nonumber \\ &=\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x,y}\tilde{p}(x,y)\log Z(x) \nonumber \\G &=\sum_{x,y}\tilde{p}(x,y)\sum_i\lambda_i f_i(x,y)-\sum_{x,y}\tilde{p}(x)\log Z(x) \label{eq:likehood} \end{align}$$

可以看出对偶函数$\Psi(\Lambda)$形式$\ref{eq:optimallambda}$和模型$p$的对数似然结果是等价的。所以整个对偶问题的求解找到的熵最大的模型$p*$其实也最大化了模型在训练样本上的似然。

参数求解

对于一般的问题一般无法用数学分析的方法求解出最大化$\Psi(\Lambda)$的$\Lambda^*$ ，一般需要用数值方法来求解。因为$\Psi(\Lambda)$是一个光滑的凸函数，所以有很多方法都可以用来求$\Lambda^*$，例如梯度下降、共轭梯度、坐标上升等方法。这里介绍的是专门针对最大熵问题设计的改进的尺度迭代算法（improved iterative scaling, IIS），该算法要求所有的特征函数$f_i(x,y)$必须非负。 IIS算法算法的关键在于求解第3步的$\Delta\lambda_i$，如果这时候$f^\#(x,y)$（表示某个样本$x,y$激活的特征函数个数）对于所有的$x,y$都一样，即$f^\#(x,y)$是一个常数$M$，那么$\Delta\lambda_i$可以按下面式子求解

$$ \Delta\lambda_i = \frac{1}{M}\log\frac{\tilde{p}(f_i)}{p_\Lambda(f_i)} $$

如果$f^\#(x,y)$不是一个常数，那么$\Delta\lambda_i$需要通过数值方法计算。一个简单快速的方法是通过牛顿法来求解，相当于这时候的目标函数 $g(\Delta\lambda_i)$就是算法第3步那个方程把右边那一项移到左边的函数，现在的目标就是要求$g(\Delta\lambda_i)=0$的$\Delta\lambda_i$，可以按下面的更新公式求

$$\begin{equation} \Delta\lambda_i^{n+1}=\Delta\lambda_i^n-\frac{g(\Delta\lambda_i^n)}{g'(\Delta\lambda_i^n)} \end{equation}$$

通过选取适当的初始$\Delta\lambda_i^0$，由于$g(\Delta\lambda_i)=0$有单根，牛顿法可以快速收敛。