MDP入门

介绍

MDP（Markov Decision Process）由5元组构成$MDP(S,A,{P_{sa}},\gamma,R)$，具体的参数介绍如下：

$S$：状态集合
$A$：动作集合
$P_{sa}$：状态转移概率分布，$P_{sa}(s')$表示在$s$状态下采取 $s$动作，转移到$s'$的概率，$P_{sa}(s')\geq0$
$\gamma$：折扣系数取值范围$0\leq\gamma\le1$
$R$：回报函数，$R:S\mapsto \mathbb{R}$

下面举一个例子来说明MDP的参数，假设一个机器人在如所描述的网格中走动，灰色代表障碍物，当机器人走到$(4,3)$位置将获得$+1$的回报，走到 $(4,2)$位置回报为$-1$。

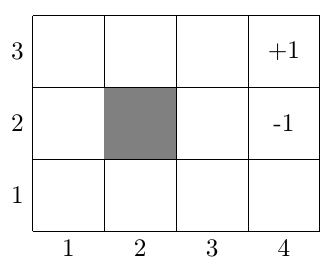
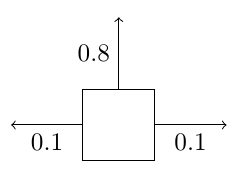
MDP简单例子动作执行受噪声干扰

如果用MDP来描述这个例子，那么$S$就有$11$中取值，机器人可能处在除了障碍物的其他位置；$A$就有$4$种取值，机器人可以往${N,S,E,W}$四个方向走；假设现在处于$[3,1]$ 位置，采取动作$N$（虽然命令机器人向前走，但是由于噪声的影响，可能机器人会向左或者向右走，如），假设$P_{[3,1]N}$分布如下 $P_{[3,1]N}([3,2])=0.8$，$P_{[3,1]N}([2,1])=0.1$，$P_{[3,1]N}([4,1])=0.1$， $P_{[3,1]N}([1,1])=0$等（除了相邻的位置，其他位置都无法到达，所以为$0$）；回报函数$R$，$R([4,2])=-1$，$R([4,3])=+1$，对于其他位置而言$R(s)=-0.02$，因为当机器人每走动一步都需要消耗电量，所以对于中间状态回报是一个比较小的负数。

对于的描述，状态的变化过程如下描述，假设$0$时刻状态是$s_0$ ，然后选择一个动作$a_0$，根据$s\_1 \thicksim P_{s_0a_0}$分布选择目标状态$s_1$，再选择动作$a_1$，根据$s\_2 \thicksim P_{s_1a_1}$选择目标状态$s_2$，依此类推状态序列。对于这个状态变化序列，可以计算总的回报值（Total Payoff）。

初始状态是$s_0$的总回报定义如下，$0\leq \gamma \le 1$：

$$R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \dots \label{eq:totalpayoff}$$

总的回报是当前的回报，加上未来的回报，但是距离当前越远回报值权重越小，为了使得总的回报值最大，我们需要选择一组最优动作序列$(a_0,a_1,\dots)$使得总回报的期望最大：

$$E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \dots] \label{eq:expectedpayoff}$$

最后还需要引入一个定义$\pi$：策略$\pi$指的是，在给定状态选择一个动作，映射关系为：$S\mapsto A$。

所以选择一个最优的动作序列，就是说要找到一个最优的$\pi$，对于能够求解出如的最优$\pi$，下面的章节会解释如何求解$\pi$。

MDP求解

本节我们需要定义几个辅助变量：$V^{\pi}$，$V^*$和$\pi^*$，下面将逐步介绍定义。

$V^\pi$

对于任意$\pi$都可以定义一个值函数$V^{\pi}$（映射关系是$S\mapsto \mathbb{R}$），$V^{\pi}$指的是从状态$s$开始并执行策略$\pi$之后所得到的总回报值的期望：

$$V^{\pi}=E\Big[R(s_0) + \gamma R(s_1) + \dots|\pi, s_0=s\Big] \label{eq:vpi}$$

下面是一个具体的例子，如是一个$\pi$，是与之对应的$V^\pi$，实际上这个策略$\pi$并不是非常好，因为对于很多状态执行该策略后趋向于走到$-1$位置而不是$+1$位置。中下面两行执行的动作使得机器人偏向走到$-1$位置，所以他们的总回报的期望值是负数，对于最上面一行偏向于走到$+1$位置，所以总回报都是正的。所以对于下两行的位置这个策略非常差，但是对于最上面那行这个策略就显得不错。

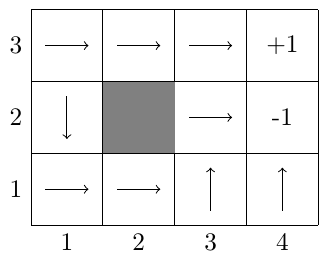
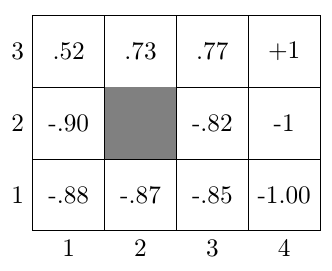
其中一个pi pi对应的V

下面要对$V^\pi$做一个推导使得$V\pi$更容易计算，这里假设当前状态$s$会转移到状态 $s'$。中的$P_{s\pi(s)}(s')$描述的是$s$状态下采取一个动作（这个动作由$\pi(s)$来确定）转移到$s'$状态的概率分布，因此式子中的求和描述的就是一个求期望的过程，总回报值的期望是当前回报加上未来回报值的期望，也称作贝尔曼方程（Bellman’s Equations）。

$$\begin{align} V^\pi(s) &= E\Big[R(s_0) + \gamma \Big(R(s_1) + \gamma R(s_2) + \dots\Big)\Big|\pi,s_0=s\Big] \cr &= R(s) + \gamma \sum_{s'}{P_{s\pi(s)}(s')V^\pi(s')} \label{eq:bellman} \end{align}$$

对于的例子，如果针对每个状态都写出方程，那么就可以得到$11$个线性方程组，并且有$11$个未知数（每个状态都有一个$V^pi(s)$），可以通过求解这个方程组得到$V^\pi$。按照的策略，我们可以计算 $[3,1]$位置的$V^\pi$：

$$\begin{split} V^\pi([3,1]) = &R([3,1]) + \cr & \gamma[0.8V\pi([3,2]) + 0.1V\pi([4,1]) + 0.1V\pi([2,1])] \end{split}$$

$V^$ 和 $\pi^$

最优值函数$V^*(s)$定义如下：

$V^*(s)$是最优值函数，值得是找到一个$\pi$使得对于所有的状态$V^\pi(s)$最大。

\begin{equation} V^*(s) = \max_x V^\pi(s) \label{eq:vstar} \end{equation}

集合和可以得到$V^*$的贝尔曼方程：

\begin{equation} V^*(s) = R(s) + \max_a \gamma \sum_{s'}{P_{sa}(s')V^*(s')} \label{eq:vstarbellman} \end{equation}

根据最优值函数的贝尔曼方程，把中的常数项$R(s)$和常数系数$\gamma$去掉（处于状态$s$时，对于所有的$a$这两个系数都相等），就可以得到最优策略$\pi^*(s)$的求解公式：

\begin{equation} \DeclareMathOperator*{\argmax}{arg\,max} \pi^*(s) = \argmax_a \sum_{s'}{P_{sa}(s')V^*(s')} \label{eq:bestpi} \end{equation}

由可以看出$\pi^*(s)$其实依赖于$V^*(s)$，所以现在的主要目标是要想办法求解 $V^*(s)$。根据的定义，最直接的方法就是穷举所有的$\pi$，但是穷举的情况会非常多，例如有$11$个状态，$4$个动作那么就有$4^{11}$种组合，搜索空间呈指数增长，不大合理，下面将介绍值迭代（Value Iteration）和策略迭代（Policy Iteration）方法来求解$V^*(s)$。

算法所描述的是值迭代的过程，初始化时对于所有的$s$对应的 $V(s)$为$0$，接着对于每个$V(s)$，这里的$V(s)$有两种更新方式。

值迭代

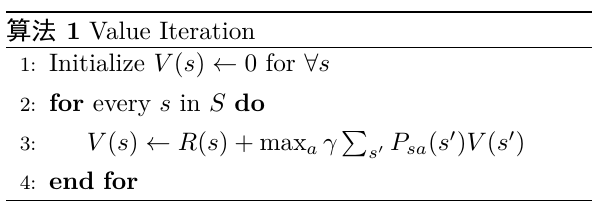
第一种是对于所有的状态计算出式子右边的部分，然后同时更新所有的$V(s)$,这种称作同步更新（Synchronous Update）；另一种叫做异步更新（Asynchronous Update），假设我们按照固定的状态顺序更新$V(s)$，那么首先会更新第1个状态的$V(s)$，接着是第2个状态的$V(s)$、第3个状态的$V(s)$、第4个状态的$V(s)$ ，如果在更新第5个状态的$V(s)$用到的$V(s')$恰好是第1、2、3、4状态的，那么我们使用的$V(s')$是前面几次迭代更新的版本。两种方法中异步更新会收敛地稍微快一点，值迭代会使得$V(s)$不断地向$V^*(s)$接近，如是最后求解出来的$V^*(s)$。

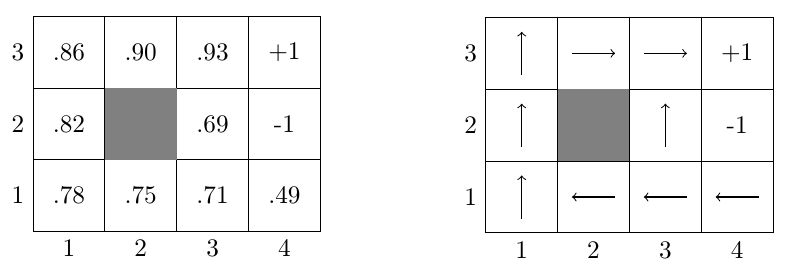
$左图是$V^*$且\gamma=.99，右图是对应的$\pi^*$$

求解出$V^*(s)$之后，根据就可以计算$\pi^*(s)$，下面举一个例子计算$\pi([3,1])$的最优策略，结合，可以计算出采取各个动作的未来总回报的期望，假设机器人碰到墙壁之后会回到原来的位置，所以机器人向$E$走的时候有$0.1$的可能性会碰到墙壁然后又返回到$[3,1]$位置。

\begin{aligned} E: & \sum_{s'}{P_{sa}(s')V^*(s')} = 0.8*0.75 + 0.1*0.69 + 0.1*0.71 = 0.74\cr N: & \sum_{s'}{P_{sa}(s')V^*(s')} = 0.8*0.69 + 0.1*0.75 + 0.1*0.49 = 0.676\cr W: & \sum_{s'}{P_{sa}(s')V^*(s')} = 0.8*0.49 + 0.1*0.69 + 0.1*0.71 = 0.532\cr S: & \sum_{s'}{P_{sa}(s')V^*(s')} = 0.8*0.71 + 0.1*0.75 + 0.1*0.49 = 0.692 \end{aligned}

对比$4$个方向的未来总回报的期望值之后，发现采取$E$动作之后得到的值最大，所以在$[3,1]$位置会采取动作$E$。对每个状态都计算最优动作之后就可以得到如所示的结果。

描述完值迭代之后，下面简单描述一下策略迭代求解$V^*(s)$，策略迭代会使得最后 $V(s)$趋近于$V^*(s)$并且$\pi(s)$趋近于$\pi^*(s)$。

策略迭代

当状态数量少的时候可以采用策略迭代，因为这时候求解贝尔曼方程比较快速，但是当状态数非常多，例如有100万个状态，那么求解贝尔曼方程的代价可能会太大，就应该考虑使用值迭代。

这里还需要讨论一下如何求解$P_{sa}$，一般来说可以用最大似然估计来估计。

\begin{equation} \begin{split} P_{sa}(s') &= \frac{\text{在}s\text{状态下采取动作a到达状态}s'\text{的次数}} {\text{在}s\text{状态下采取动作}a\text{的次数}} \cr &\Big(\text{如果得到}\frac{0}{0}\text{的情况就用}\frac{1}{|s|}\text{替换}\Big) \end{split} \label{eq:psa} \end{equation}

求解过程总结

把上文提到的求解$V^*(s)$、$\pi^*(s)$和$P_{sa}$的方法结合起来就可以构成一个完整的求解MDP的方法。首先采取策略$\pi$之后可以观测到一些状态转移的数据，用这些数据来重新估计$P_{sa}$，接着用值迭代的方式来求解当前$\pi$和$P_{sa}$前提下的$V^*(s)$（值迭代的初始$V(s)$可以使用上一轮迭代的$V^*(s)$），最后再利用这个$V^*(s)$来更新$\pi$。整个过程

Life in a Nutshell

介绍

MDP求解

\(V^\pi\)

\(V^\) 和 \(\pi^\)

求解过程总结

Comments

介绍

MDP求解

\(V^\pi\)

\(V^*\) 和 \(\pi^*\)

求解过程总结

Comments

\(V^\) 和 \(\pi^\)